PENGERTIAN KORELASI

Secara sederhana, korelasi dapat diartikan sebagai hubungan. Namun ketika dikembangkan lebih jauh, korelasi tidak hanya dapat dipahami sebatas pengertian tersebut. Korelasi merupakan salah satu teknik analisis dalam statistik yang digunakan untuk mencari hubungan antara dua variabel yang bersifat kuantitatif. Hubungan dua variabel tersebut dapat terjadi karena adanya hubungan sebab akibat atau dapat pula terjadi karena kebetulan saja. Dua variabel dikatakan berkolerasi apabila perubahan pada variabel yang satu akan diikuti perubahan pada variabel yang lain secara teratur dengan arah yang sama (korelasi positif) atau berlawanan (korelasi negatif).

Dalam Matematika, korelasi merupakan ukuran dari seberapa dekat dua variabel berubah dalam hubungan satu sama lain. Sebagai contoh, kita bisa menggunakan tinggi badan dan usia siswa SD sebagai variabel dalam korelasi positif. Semakin tua usia siswa SD, maka tinggi badannya pun menjadi semakin tinggi. Hubungan ini disebut korelasi positif karena kedua variabel mengalami perubahan ke arah yang sama, yakni dengan meningkatnya usia, maka tinggi badan pun ikut meningkat.

Sementara itu, kita bisa menggunakan nilai dan tingkat ketidak hadiran siswa sebagai contoh dalam korelasi negatif. Semakin tinggi tingkat ketidak hadiran siswa di kelas, maka nilai yang diperolehnya cenderung semakin rendah. Hubungan ini disebut korelasi negatif karena kedua variabel mengalami perubahan ke arah yang berlawanan, yakni dengan meningkatnya tingkat ketidak hadiran, maka nilai siswa justru menurun.

Kedua variabel yang dibandingkan satu sama lain dalam korelasi dapat dibedakan menjadi variabel independen dan variabel dependen. Sesuai dengan namanya, variabel independen adalah variabel yang perubahannya cenderung di luar kendali manusia. Sementara itu variabel dependen adalah variabel yang dapat berubah sebagai akibat dari perubahan variabel indipenden. Hubungan ini dapat dicontohkan dengan ilustrasi pertumbuhan tanaman dengan variabel sinar matahari dan tinggi tanaman. Sinar matahari merupakan variabel independen karena intensitas cahaya yang dihasilkan oleh matahari tidak dapat diatur oleh manusia. Sedangkan tinggi tanaman merupakan variabel dependen karena perubahan tinggi tanaman dipengaruhi langsung oleh intensitas cahaya matahari sebagai variabel indipenden.

MACAM-MACAM KORELASI

Korelasi sebagai sebuah analisis memiliki berbagai jenis menurut tingkatannya. Beberapa tingkatan korelasi yang telah dikenal selama ini antara lain adalah korelasi sederhana, korelasi parsial, dan korelasi ganda. Berikut ini adalah penjelasan dari masing-masing korelasi dan bagaimana cara menghitung hubungan dari masing-masing korelasi tersebut.

1. Korelasi Sederhana

Korelasi Sederhana merupakan suatu teknik statistik yang dipergunakan untuk mengukur kekuatan hubungan antara 2 variabel dan juga untuk dapat mengetahui bentuk hubungan keduanya dengan hasil yang bersifat kuantitatif. Kekuatan hubungan antara 2 variabel yang dimaksud adalah apakah hubungan tersebut erat, lemah, ataupun tidak erat. Sedangkan bentuk hubungannya adalah apakah bentuk korelasinya linear positifataupun linear negatif.

Di antara sekian banyak teknik-teknik pengukuran asosiasi, terdapat dua teknik korelasi yang sangat populer sampai sekarang, yaitu Korelasi Pearson Product Moment dan Korelasi Rank Spearman. Lalu apa perbedaan di antara keduanya?

Korelasi Pearson Product Moment adalah korelasi yang digunakan untuk data kontinu dan data diskrit. Korelasi pearson cocok digunakan untuk statistik parametrik. Ketika data berjumlah besar dan memiliki ukuran parameter seperti mean dan standar deviasi populasi.

Korelasi Pearson menghitung korelasi dengan menggunakan variasi data. Keragaman data tersebut dapat menunjukkan korelasinya. Korelasi ini menghitung data apa adanya, tidak membuat ranking atas data yang digunakan seperti pada korelasi Rank Spearman. Ketika kita memiliki data numerik seperti nilai tukar rupiah, data rasio keuangan, tingkat pertumbuhan ekonomi, data berat badan dan contoh data numerik lainnya, maka Korelasi Pearson Product Moment cocok digunakan.

Sebaliknya, Koefisien Korelasi Rank Spearman digunakan untuk data diskrit dan kontinu namun untuk statistik nonparametrik. Koefisien korelasi Rank Spearman lebih cocok untuk digunakan pada statistik nonparametrik. Statistik nonparametrik adalah statistik yang digunakan ketika data tidak memiliki informasi parameter, data tidak berdistribusi normal atau data diukur dalam bentuk ranking. Berbeda dengan Korelasi Pearson, korelasi ini tidak memerlukan asumsi normalitas, maka korelasi Rank Spearman cocok juga digunakan untuk data dengan sampel kecil.

Korelasi Rank Spearman menghitung korelasi dengan menghitung ranking data terlebih dahulu. Artinya korelasi dihitung berdasarkan orde data. Ketika peneliti berhadapan dengan data kategorik seperti kategori pekerjaan, tingkat pendidikan, kelompok usia, dan contoh data ketegorik lainnya, maka Korelasi Rank Spearman cocok digunakan. Korelasi Rank Spearman pun cocok digunakan pada kondisi dimana peneliti dihadapkan pada data numerik (kurs rupiah, rasio keuangan, pertumbuhan ekonomi), namun peneliti tidak memiliki cukup banyak data (data kurang dari 30).

2. Korelasi Parsial

Korelasi parsial adalah suatu metode pengukuran keeratan hubungan (korelasi) antara variabel bebas dan variabel tak bebas dengan mengontrol salah satu variabel bebas untuk melihat korelasi natural antara variabel yang tidak terkontrol. Analisis korelasi parsial (partial correlation) melibatkan dua variabel. Satu buah variabel yang dianggap berpengaruh akan dikendalikan atau dibuat tetap (sebagai variabel kontrol).

Sebagai contoh misalnya kita akan meneliti hubungan variabel X2 dan variabel bebas Y, denganX1 dikontrol (korelasi parsial). Disini variabel yang dikontrol (X1) dikeluarkan atau dibuat konstan. Sehingga X2’ = X2 – (b2X1 + a2 ) dan Y’ = Y – (b1 X1 +a1 ), tetapi nilai a dan b didapatkan dengan menggunakan regresi linear. Setelah hasilnya diperoleh, kemudian dicari regresi X2‘ dengan Y’ dimana : Y’ = b3X2’ +a3. Korelasi yang didapatkan dan sejalan dengan model-model di atas dinamakan korelasi parsial X2 dan Y sedangkan X1 dibuat konstan.

Nilai korelasi berkisar antara 1 sampai -1, nilai semakin mendekati 1 atau -1 berarti hubungan antara dua variabel semakin kuat. Sebaliknya, jika nilai mendekati 0 berarti hubungan antara dua variabel semakin lemah. Nilai positif menunjukkan hubungan searah (X naik, maka Y naik) sementara nilai negatif menunjukkan hubungan terbalik (X naik, maka Y turun).

Data yang digunakan dalam korelasi parsial biasanya memiliki skala interval atau rasio. Berikut adalah pedoman untuk memberikan interpretasi serta analisis bagi koefisien korelasi menurut Sugiyono:

0.00 - 0,199 = sangat rendah

0,20 - 0,3999 = rendah

0,40 - 0,5999 = sedang

0,60 - 0,799 = kuat

0,80 - 1,000 = sangat kuat

3. Korelasi Ganda

Korelasi ganda adalah bentuk korelasi yang digunakan untuk melihat hubungan antara tiga atau lebih variabel (dua atau lebih variabel independen dan satu variabel dependent. Korelasi ganda berkaitan dengan interkorelasi variabel-variabel independen sebagaimana korelasi mereka dengan variabel dependen.

Korelasi ganda adalah suatu nilai yang memberikan kuatnya pengaruh atau hubungan dua variabel atau lebih secara bersama-sama dengan variabel lain. Korelasi ganda merupakan korelasi yang terdiri dari dua atau lebih variabel bebas (X1,X2,…..Xn) serta satu variabel terikat (Y). Apabila perumusan masalahnya terdiri dari tiga masalah, maka hubungan antara masing-masing variabel dilakukan dengan cara perhitungan korelasi sederhana.

Korelasi ganda memiliki koefisien korelasi, yakni besar kecilnya hubungan antara dua variabel yang dinyatakan dalam bilangan. Koefisien Korelasi disimbolkan dengan huruf R. Besarnya Koefisien Korelasi adalah antara -1; 0; dan +1.

Besarnya korelasi -1 adalah negatif sempurna yakni terdapat hubungan di antara dua variabel atau lebih namun arahnya terbalik, +1 adalah korelasi yang positif sempurna (sangat kuat) yakni adanya sebuah hubungan di antara dua variabel atau lebih tersebut, sedangkan koefisien korelasi 0 dianggap tidak terdapat hubungan antara dua variabel atau lebih yang diuji sehingga dapat dikatakan tidak ada hubungan sama sekali.

PENGERTIAN REGRESI

       Sir Francis Galton (1822 – 1911), memperkenalkan model peramalan, penaksiran, atau pendugaan, yang selanjutnya dinamakan regresi, sehubungan dengan penelitiannya terhadap tinggi badan manusia. Penelitian tersebut membandingkan antara tinggi anak laki-laki dan tinggi badan ayahnya. Galton menunjukkan bahwa tinggi badan anak laki-laki dari ayah yang tinggi setelah beberapa generasi cenderung mundur (regressed) mendekati nilai tengah populasi. Dengan kata lain, anak laki-laki dari ayah yang badannya sangat tinggi cederung lebih pendek dari pada ayahnya, sedangkan anak laki-laki dari ayah yang badannya sangat pendek cenderung lebih tinggi dari ayahnya. (Ronal E. Walpole). Analisis regresi digunakan untuk menentukan bentuk (dari) hubungan antar variabel. Tujuan utama dalam penggunaan analisis ini adalah untuk meramalkan atau menduga nilai dari satu variabel dalam hubungannya dengan variabel yang lain yang diketahui melalui persamaan garis regresinya. (Iqbal Hasan).

       Adakalanya, setelah kita memperoleh data berdasarkan sampel, kita ingin menduga nilai dari suatu variabel Y yang bersesuaian dengan nilai tertentu dari variabel X. Hal ini diperoleh dengan menaksir nilai Y dari kurva kuadrat minimum yang sesuai dengan data yang kita himpun dari sampel. Kurva yang diperoleh dan kita bentuk dari data sampel itu disebut kurva regresi Y terhadap X, karena Y diduga dari X. (Murray R. Spiegel).

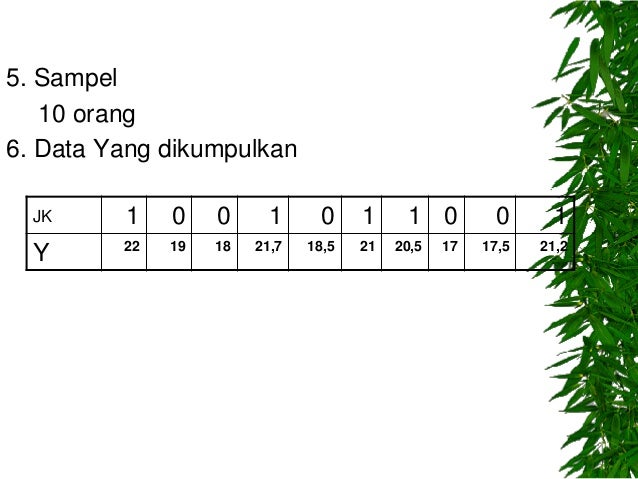
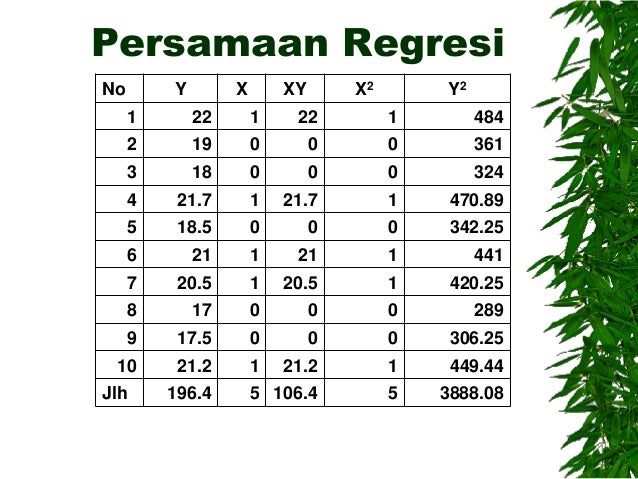
        Dalam melakukan analisis regresi, sebagian besar mahasiswa biasanya tidak melakukan pengamatan populasi secara langsung. Hal itu dilakukan selain pertimbangan waktu, tenaga, juga berdasarkan pertimbangan biaya yang relatif besar jika melakukan pengamatan terhadap populasi. Dalam hal ini, lazimnya digunakan persamaan regresi linier sederhana sampel sebagai penduga persamaan regresi linier sederhana populasi dengan bentuk persamaan seperti berikut : y = a + bX. Dan karena antara Y dan X memiliki hubungan, maka nilai X dapat digunakan untuk menduga atau meramal nilai Y. X dinamakan variabel bebas karena variabel ini nilai-nilainya tidak bergantung pada variabel lain. Dan Y disebut variabel terikat juga karena variabel yang nilai-nilainya bergantung pada variabel lain. Hubungan antar variabel yang akan dipelajari disini hanyalah hubungan linier sederhana, yakni hubungan yang hanya melibatkan dua variabel (X dan Y) dan berpangkat satu. (Iqbal Hasan).

       Regresi sederhana, adalah bentuk regresi dengan model yang bertujuan untuk mempelajari hubungan antara dua variabel, yakni variabel independen (bebas) dan variabel dependen (terikat). Jika ditulis dalam bentuk persamaan, model regresi sederhana adalah y = a + bx, dimana, y adalah variabel takbebas (terikat), X adalah variabel bebas, a adalah penduga bagi intercept (α), b adalah penduga bagi koefisien regresi (β). Atau dengan kata lain α dan β adalah parameter yang nilainya tidak diketahui sehingga diduga melalui statistik sampel. (Sambas dan Maman)

       Menurut kelaziman, dalam ilmu statistika ada dua macam hubungan antara dua variabel yang relatif sering digunakan, yakni bentuk hubungan dan keeratan hubungan. Bentuk hubungan bisa diketahui melalui analisis regresi, sedangkan keeratan hubungan dapat diketahui dengan analisis korelasi. Analisis regresi dipergunakan untuk menelaah hubungan antara dua variabel atau lebih, terutama untuk menelusuri pola hubungan yang modelnya belum diketahui dengan baik, atau untuk mengetahui bagaimana variasi dari beberapa variabel independen mempengaruhi variabel dependen dalam suatu fenomena yang komplek. Jika X1, X2, ...., Xn, adalah variabel-variabel independen dan Y adalah variabel dependen, maka terdapat hubungan fungsional antara X dan Y, dimana variasi dari X akan diiringi pula oleh variasi dari Y. Jika dibuat secara matematis hubungan itu dapat dijabarkan sebagai berikut: Y = f(X1, X2, ....., Xn, e), dimana Y adalah variabel dependen (tak bebas), X adalah variabel independen (bebas) dan e adalah variabel residu (disturbace term).

         Berkaitan dengan analisis regresi ini, setidaknya ada empat kegiatan yang lazim dilaksanakan yakni : (1) mengadakan estimasi terhadap parameter berdasarkan data empiris, (2) menguji berapa besar variasi variabel dependen dapat diterangkan oleh variasi independen, (3) menguji apakah estimasi parameter tersebut signifikan atau tidak, dan (4) melihat apakah tanda magnitud dari estimasi parameter cocok dengan teori. (Moh. Nazir).

        Hubungan antar variabel dapat berupa hubungan linier ataupun hubungan tidak linier. Misalnya, berat badan orang dewasa sampai pada tahap tertentu bergantung pada tinggi badan, keliling lingkaran bergantung pada diameternya, dan tekanan gas bergantung pada suhu dan volumenya. Atau dalam ilmu pemasaran, nilai penjualan akan bergantung pada biaya promosi. Hubungan-hubungan itu bila dinyatakan dalam bentuk matematis akan memberikan persamaan-persamaan tertentu. Untuk dua variabel, hubungan liniernya dapat dinyatakan dalam bentuk persamaan linier, yakni: Y = a + bX. Hubungan antara dua variabel pada persamaan linier jika digambarkan secara (scatter diagram), semua nilai Y dan X akan berada pada suatu garis lurus. Dan dalam ilmu ekonomi, garis itu dinamakan garis regresi. (Iqbal Hasan).